What is the Coriolis force
The Coriolis force has a huge impact on the weather. It's the power that spins cyclones and anticyclones, and it also affects the direction of trade winds and sea currents. The force is named after the scientist Gaspard-Gustave Coriolis, who discovered it. In this new lesson of the Windy.app Meteorological Textbook (WMT) and newsletter for better weather forecasting you will learn more about Coriolis force.
What is Coriolis force?
If a body moves on the surface of the Earth, it always deflects to the right in the Northern Hemisphere and to the left in the Southern Hemisphere. In general, the Coriolis force acts on all moving objects (even on people walking). Let’s take air as an example.
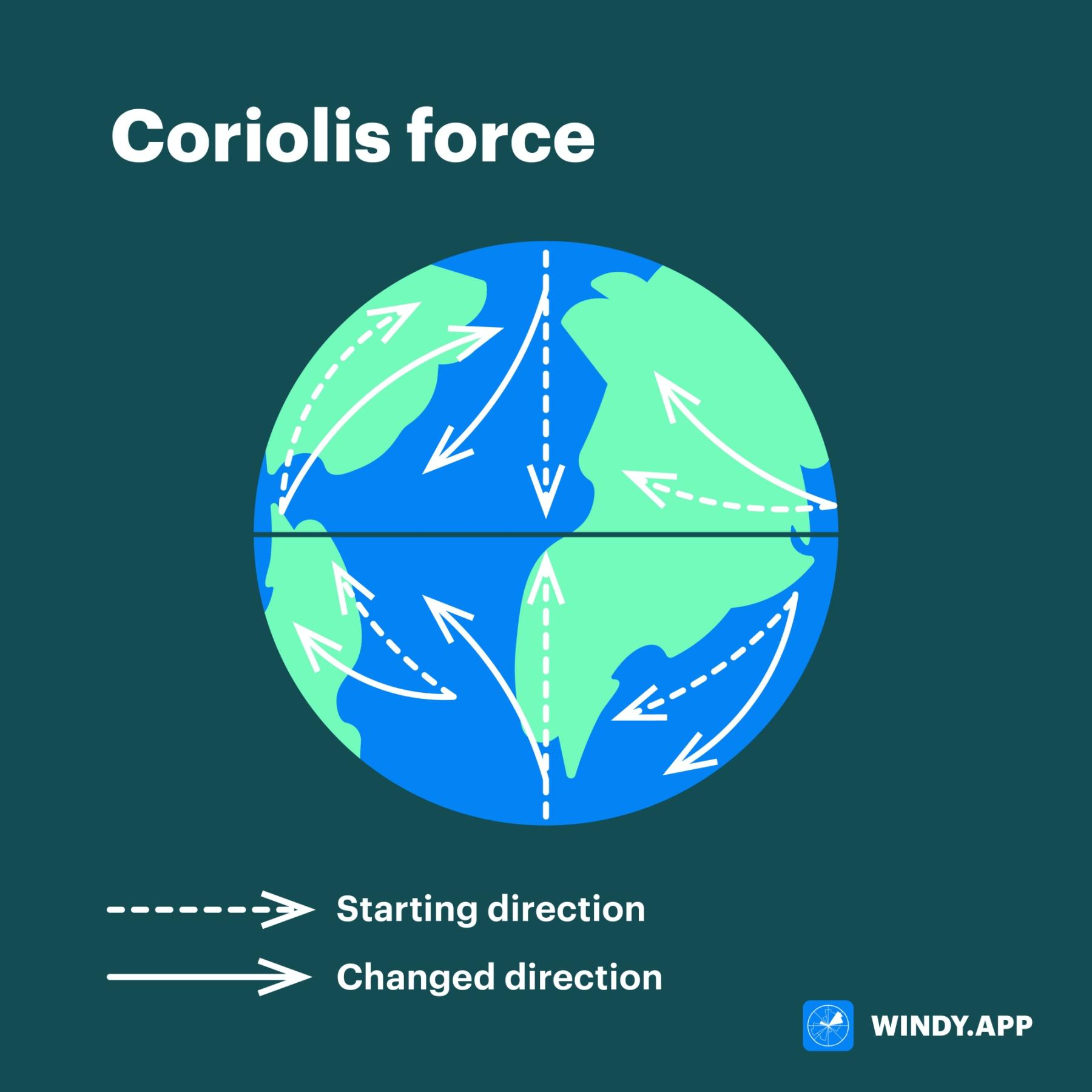
The Coriolis force. Illustration: Valerya Milovanova / Windy.app
Why can't air move straight?
The Coriolis force occurs because our planet rotates around its axis and all points on the planet's surface move around the axis of the Earth's rotation. But they all move at different speeds.
Look at the picture — point A in the picture will move around the axis faster than point B.
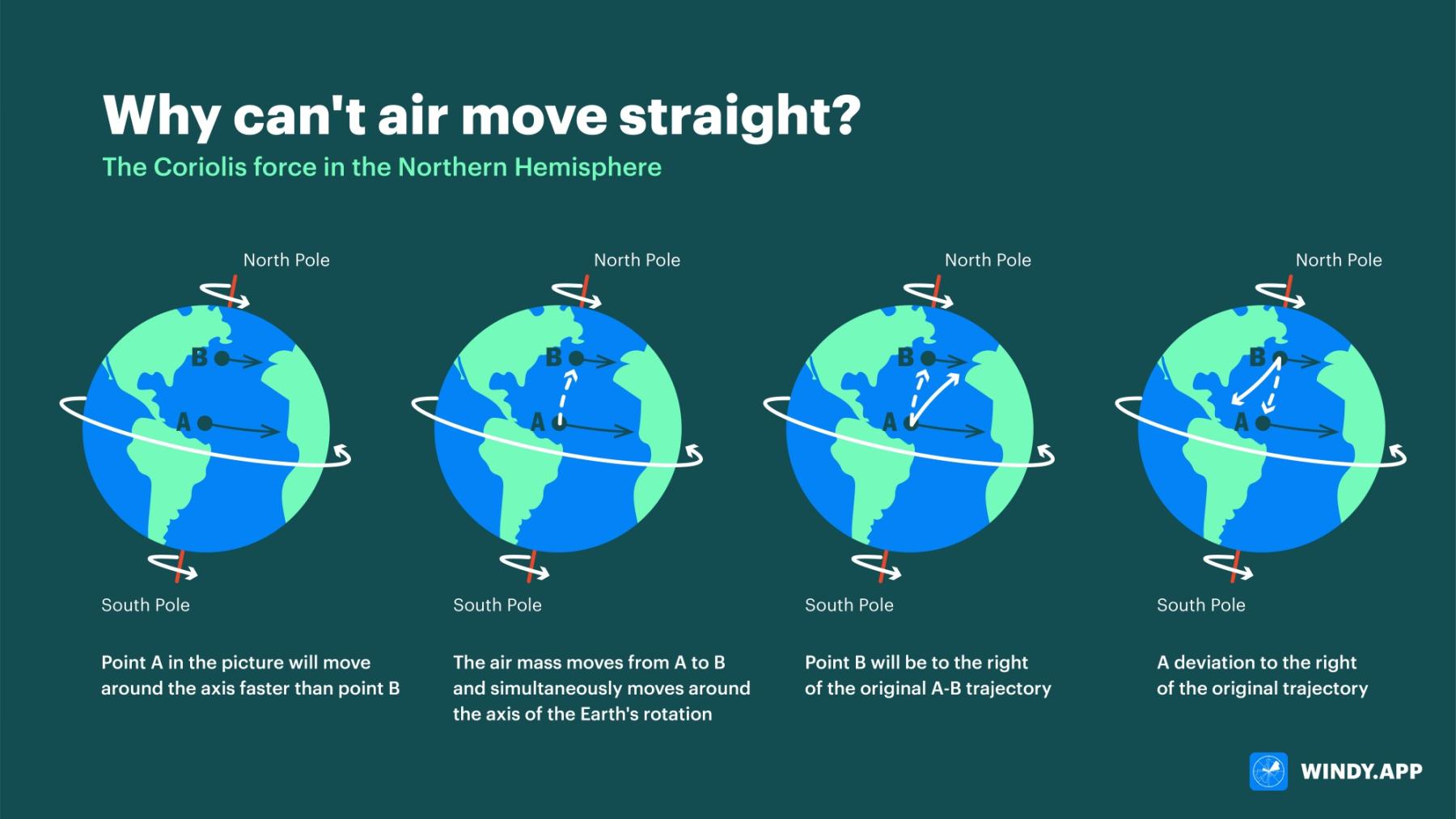
It’s because the Earth is a sphere. Each point, rotating around the axis, makes a circle, and the center of this circle is on the axis of the Earth’s rotation.
It turns out that if points are at different latitudes (like A and B), they make circles of different radii. The closer to the pole, the smaller is the radius and the shorter is the length of the circle.
The longest circle will be on the equator, which means a point on the equator has to travel a very long distance during one revolution of the Earth around the axis. And a point close to the pole has to travel a really short distance.
The closer a point is to the equator, the bigger is the circle it makes during the rotation together with the planet.
The time is the same for all points, and the distance is different. Therefore those points which are closer to the equator have to move faster.
Point A has to make a much longer circle during the same time as point B, so it moves faster.
The closer a point is to the equator, the faster it moves around the axis.
Now let’s imagine that an air mass goes from point A to point B. Let’s look at this movement.
The atmosphere rotates with the planet, so the air mass moves from A to B and simultaneously moves around the axis of the Earth’s rotation.
As it moves in two directions at once, it has two different speeds. Let’s call the speed at which the air mass rotates around the axis of the Earth’s rotation «planetary», and the speed at which the air mass moves from point A to point B can be optional.
Now remember that the speed of the rotation of the planet is not the same at different latitudes: point A rotates faster than point B. This is the most important starting condition. Because of this, the air mass at point A also rotates faster than point B (because, as we have already noted, the atmosphere rotates with the planet). As a result, when the air mass is at point B, its planetary speed will still be higher than that of point B.
If the air mass does not go beyond point B, then after a while its «planetary» speed will be the same as that of point B. But the «planetary» speed of the air mass is originally higher!
It turns out that at point B, the air mass will rotate faster than point B itself, and it will sort drift forward. As a result, it will be to the right of the original A-B trajectory.
When moving from high latitudes to lower latitudes, the opposite happens: the air mass does not go faster the planet, but falls behind, and again it looks like a deviation to the right of the original trajectory.
This is what happens in the Northern Hemisphere.
In the Southern Hemisphere, moving objects deflect to the left, on the contrary. The Coriolis force is infinite at the poles and gradually diminishes towards the equator. At the equator, the Coriolis force is equal to zero.
Text: Windy.app team
Illustration: Valerya Milovanova, an illustrator with a degree from the British Higher School of Art an Design (BHSAD) of Universal University
Cover photo: Unsplash / Unsplash
You will also find useful
Latest News
Professional Weather App
Get a detailed online 10 day weather forecast, live worldwide wind map and local weather reports from the most accurate weather models.
Compare spot conditions, ask locals in the app chat, discover meteo lessons, and share your experience in our Windy.app Community.
Be sure with Windy.app.